Walking into the PDP process, this domain probably worried me the most. Getting a Ph.D. might give me an overall knowledge of mathematics as a field higher than that of a typical high school teacher but also gave me an awareness of just how little I actually know. It also gave me no knowledge of high school teaching practices and theory. There are real issues with hiring a Ph.D. to teach high school, especially a freshly minted one. My own experience with professors in college taught me that having a Ph.D. does not mean you are a good teacher, as so many are more interested in research than teaching. I know full well how competitive the job market is for college jobs and many Ph.D.’s will look to teach high school as a temporary job until they can pump out a couple more papers and find a college job. This outlook will inevitably lead to a poor teacher, as teaching high school is a full time job and can only be done effectively if you have an actual passion for it. Ever since I came to EPS, I have been trying to prove that I am here for the right reasons, that teaching is a calling and I belong here.
I want to give a quote from Adrienne Behrmann here to illustrate my evolution in the math discipline. She gave this in response to me asking how I can improve my practice:
“In your first couple of years, I would have encouraged you to be more proactive in speaking out and expressing your viewpoint, but with each year, your confidence has increased to the point where you are very comfortable speaking out and contributing in a very positive and helpful way to discussions.”
I give this quote because I find it revealing into my thought process over the years. When I got to EPS, I was very quiet when it came to discipline meetings. I only like to speak when I feel like I have something to offer, and what did I have to offer to such established and phenomenal teachers like Adrienne Behrmann, Steve Fassino, or Randy Reina? I tried to spend those years listening to those teachers, learning from them and trying to prove that, at the very least, I was here for the right reasons.
A piece of the belief that I have nothing to offer the math discipline still exists. Adrienne might have retired and Randy will join her once we stop dragging him back, but the discipline has added absolute powerhouses since I started, teachers with over a decade of experience and amazing knowledge of mathematical education theory. While I am improving my knowledge of the research and accepted practices of teaching math at the high school level, I still do not hold a candle to such exceptional teachers.
On the other hand, I have come to realize that while I may not have much to offer on teacher practices yet, I do have a wealth of knowledge to offer on math itself and how to prepare students for college. My background in math has given me insight into the connections between mathematical topics and broad overview of when students might see things again in the future. Having spent time in graduate school rooming with engineers and working with other departments, I also have a good deal of knowledge on how to integrate with math with other disciplines. All these skills I can bring to the table in a discipline meeting.
Having taught at the college level, I know the expectations that will be placed on our students and can help ready them for that challenge. I can teach them, as I do in Advanced Topics and in my seminar on the Millenium Problems, fields of mathematics beyond Calculus, introducing them to the world of modern mathematics and what mathematics actually work on in the present. I can also establish connections between math and other disciplines, helping students to see that math will be present in their lives long after they finish taking math classes.
Finally, although quite alarming to me, I offer some amount of institutional memory. With Randy’s retirement becoming fully official next year (or at least for his sake, I hope so), I am the third most tenured teacher in the math discipline and, accounting for the fact that one of the more tenured teachers is Adam Kruger, who switched into our discipline this year after teaching Physics, the second most tenured math teacher. As I am only in year six at EPS, it is alarming how much turnover in the discipline that has occurred, but that does mean I have insight into the evolution of math education at EPS. I sincerely hope that the turnover in math stabilizes, as I believe we have had a new math teacher every year I have worked here, but at the very least, I will be able to offer a degree of institutional knowledge matched only by Steve and Adam, and only by Steve when it comes to the math discipline itself.
Curriculum | Discipline Design
(1) designs and implements courses that reflect teacher mastery of their academic discipline and its teaching methodologies
In terms of mastery of mathematics, I think my background gives me a unique insight. I hold a Ph.D. in mathematics and while that does not mean I have an extensive knowledge of mathematics teaching methodologies, it does mean I have experience with math at a level beyond a usual math teacher. This has given me extensive insight into where students might encounter these topics in other fields of study. It has also given me a background in the development of mathematical concepts historically. Having also taught at the college level, I also have knowledge of what studying math at the college level looks like and what specific classes certain majors might require in math.
Advanced Topics is a course I have taught for the last five years and is probably the best example I have of implementing a course that reflect my mastery of mathematics. This class is supposed to cover topics beyond Calculus in math and I have treated each trimester as an opportunity to introduce new topics. The first two trimester cover topics that I believe are not only significant mathematically but are also the topics with the most connections to other fields, with the sole exception of statistics which is its own class in our curriculum. The first trimester covers Linear Algebra, which gets students comfortable with vectors and matrices. These are essential for computer programming and outside of statistics, are the most extensively used mathematical objects in other fields. This trimester is also used to introduce students to higher level symbolic manipulation and non-geometry proof-based writing, essential ingredients to a mathematics major and usually required topics for engineering fields.
The second trimester covers Differential Equations. This class helps tie together everything students have learned in math. It extends the ideas of Calculus to more real-world scenarios, forming the foundation of most of Physics and Engineering sciences. I also make sure to introduce the use of matrices to solving these equations, tying back to what we did in the first trimester and also giving them insight into how computer systems can be used to model solutions. In total, these two trimesters together with our Calculus and Advanced Calculus classes should place our student at the level of a sophomore in college in terms of the math they have been exposed to. The third trimester of this course is often left for the students to pick their own topic, but those topics are always higher level as well and have covered such disparate topics as Multivariable Calculus, Game Theory, Number Theory, Complex Analysis, Combinatorics and Probability, and Graph Theory.
This course is taught in a college style, probably more reliant on lecture than a typical EPS course. Since this course is the last course in our math curriculum, taken mostly by seniors who are motivated to take STEM classes in college, it seems important to me to give them experience in a college lecture style. I also want students in Topics to start to see the connections math has to other disciplines, so I have made sure to include one application questions on each test this year, having Chemistry and Material Science questions on Linear Algebra tests, Physics and retirement account planning questions on Differential Equations tests, and a cipher decryption question on the Number Theory test.
One thing that I have noted is that the alumni I have talked to have all said they felt well-prepared taking math classes in college. This sentiment has been reflected in my conversations with Bart Gummere as well. I also offer this quote from Eric Zhou, an alumni from the class of 2023 I bumped into in the airport during the winter holiday break: “All the topics we covered in Advanced Topics were exactly what we did my first year in college.” I also offer this email I received from Hazel Goetsch, another alumni from the class of 2023:
You may notice that I have not really mentioned the idea of mathematical teaching methodologies here, although I did have my rationale for teaching Advanced Topics the way I do. The truth is, I still need to improve my knowledge of mathematical teaching methodologies. I do not have a background in the educational debates and theories of teaching math, instead being sent into a college classroom with no formal training and then transitioning straight from college teaching to high school. I am still working my way up to speed on these things and probably can use more training on the formalness of math education, especially when it comes to teaching at the high school level.
(2) designs and implements courses framed by the school’s pedagogical tenets – inquiry, experience, and integration
Inquiry is a challenge for me, as my experience with inquiry prior to coming to EPS was very much rooted in the hand students a scaffolded worksheet to lead them to “discovering” a big idea and then ask “guiding questions” if they got stuck until they got back on track before giving a quick five minute explanation at the end of class. In truth, I am not a fan of this model at the high school level, as it still gives the impression of handing students a worksheet for the day and it lacks guardrails to prevent productive struggle from becoming unproductive, notably because the only time direct instruction is given is at the very end of class. I still struggle to recognize that inquiry is more than this mode alone and a lot of what I do is blending inquiry and direct instruction even if it feels to me like just the latter. An example of this discrepancy is the same one I gave in the Pedagogical Practices domain:
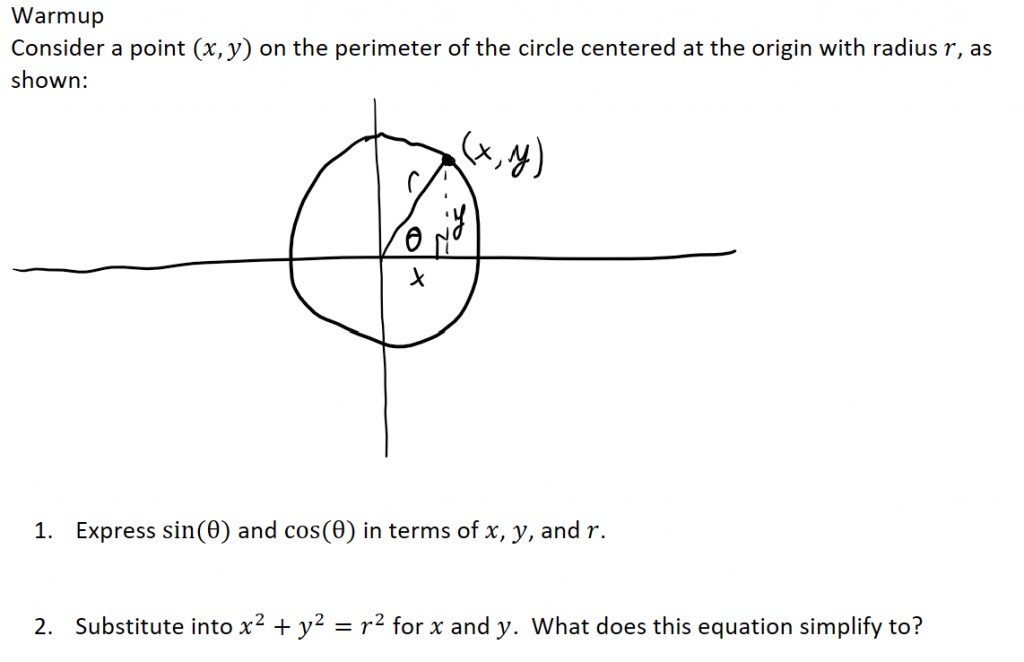
When designing this problem, which is supposed to lead students to the Pythagorean identity, it felt to me like I was doing direct instruction, yet it was pointed out to me during my observation follow-up with John Stegeman that this is actually inquiry. I have started to realize that I give pockets of inquiry during my class and that these pockets coupled with dedicated practice time constitute the majority of time spent in class, but I still think of myself as a direct instruction teacher.
Having said that, there are numerous ways students can take the lead in my class. I often provide challenge problems for students who might feel bored by the regular material and I strive to make my review significantly more challenging than examinations. Time is always given in class for students to think about and try problems and I try to give that same freedom outside of class as well. I will make time for students who need additional support if they request it and will continue to do so for anything math related outside the classroom, whether that be for AP testing, students needing to ask questions outside of their current teacher’s availability, independent studies, or even for alumni who simply want to discuss the research they are working on in college.
As for experience, my classes are designed to experience math in a way that prepares students for college and beyond. My classes are taught in a college style, getting students experience in not just the mathematics they might study but in the expectations professors will place upon them. Collaboration and critical thinking are emphasized, as students are expected to discuss problems with their peers and make connections and extensions on their own. As I have gotten more comfortable teaching at the high school level, more projects and labs have been introduced so students get more hands on experience. In Calculus this year, we have featured numerous inquiry based hands on activities to help students play with major ideas before they are fully introduced, leading ultimately to a final project where they have to create something creative of their own design, like a song, poem, board game, or art piece, that illustrates a concept of calculus we covered this year. Brandon Smith, my co-teacher on these labs before he left, said “We worked on the project to introduce kids to derivatives. We really took our time with this and your contributions to those lessons were invaluable. You have a vision for where topics can go and for excellent questions that distill an idea down to it’s core… these kinds of questions or examples that make for wonderful inquiry projects. I think you have wonderful vision and wonderful patience in the introduction of topics and in that lesson in particular, I appreciated how we took the time, made the time, to take it slow and give this monumental topic it’s time in the sun.”
As for integration, it is hard to collaborate with other disciplines as our math classes are mixed grade level. That makes it hard, as we cannot presume student knowledge of another discipline. That said, I do try to give those connections to students as best I can. I have given an application style question on every test this year so far in Advanced Topics and one of the labs we designed in Calculus specifically concerned the Physics idea of speed of a car. The timing of that lab actually worked out well, as the juniors in Calculus all mentioned that Physics was doing something similar at that time, giving a nice synergy between the classes, while still emphasizing the difference between the classes, as we prioritized slightly different things in the experiments. To give some evidence of integration, I offer this statement by Anne Duffy: “Even though I am not technically in the math discipline now, we have still had multiple conversations about the math sequence and program. We have mainly chatted about applications in math and how that applies to science or what I observe as students lack of transfer of their knowledge in math and the application in chemistry. We mainly ponder and wonder when we chat. But I have seen you take that a step further by engaging with science faculty to develop and write application questions for your classroom even on assessments. This again is reenforcing the students’ mathematical thinking and also demonstrating that there is clear application to what they are learning.”
(3) collaboratively designs and evolves course curricula that are reflective of their academic discipline’s philosophy and derivative of the school’s overarching philosophy
Every year for Back To School Night, the math disciplines revises and hands out a document that seeks to explain our overarching philosophy. It is a document I have had a small hand in editing over my six years here and is something I truly believe in. I offer it below to give a foundation of our discipline thinking:
All of these philosophies are things I try to incorporate into my classroom. I truly believe that there is no such thing as a “math person” and everyone can learn and enjoy math. While I am limited by the time constraints of class and the need to prepare students to take the next math class in the sequence, I try to give as much time as I can to students to explore the topics and come to understanding them at their own pace. Persistence and effort are the most important ingredients to learning, although I have to balance this with the need to have students prepared not just for the next math class in the sequence but for college and life beyond EPS.
My classes are designed to create a comfortable environment for students to make mistakes in. I try to return assignments and give feedback within the seven day cycle as prescribed by the school. Homework is done on a completion basis so students can make mistakes in a low stakes environment. Solutions are distributed immediately upon the homework being due so students can then check their work. DESMOS is available to the students during work time so students have access not just to a calculator but visualization. Students are free to work in any manner they see fit and collaborating with tablemates during this time in encouraged.
During my time here at EPS, I have taught Pre-Calculus, Calculus, Advanced Calculus, and Advanced Topics in Mathematics. At no point has my schedule remained stable for two years. That variability in the classes I teach has given me an overarching insight into the end of the math curriculum here in a way that I think is unique to our discipline. I have helped facilitate a progression amongst these classes in regards to development, helping to align practices so that students progressively see more emphasis placed on test outcomes with less ability to improve scores through correction as they move through the curriculum. This progression helps create a nice developmental path for students as they move through the school while preparing them for college. By establishing norms and behaviors at the lower levels, we can slowly place less emphasis on teaching them to students and progressively give them greater ownership of their education.
In terms of collaboration, I have endeavored to be a true team player in the math department. I know that while I have a great deal of knowledge of math as a field, I still have much to learn in the field of math education. When the time comes and I feel like I have something to contribute, I will, but it is important to also listen to my fellow teachers and respect their expertise as well. To give an idea of how I am as a collaborator, I offer the following insights from other teachers in my discipline as to how I am to work with as co-teacher as well as how I contribute to the math discipline:
From Adrienne Behrmann:
- You were great to work with as you are organized, efficient, responsive, and always willing to help out in times of need. You often ( and still ) help me out when I need advice on how to approach a particular math problem. You are extremely knowledgeable in your subject and you are able to impart that knowledge clearly and unambiguously. You are also very patient and caring.
- We collaborated several times on the Calculus course, deciding which material to cover and the best approach to teaching it. We often talked about scope and sequence in our math discipline meetings and you offered valuable input into those discussions.
From Sarah Aguiar
- we are on the opposite ends of the math spectrum, but we have a lot of the same issues like no one to partner with. We share a kindship in that respect. You also contribute well and regularly o the math meetings, always seeking to improve the program and consider student needs before making program changes. You run the numbers each year for how many sections we need and that is super helpful with planning.
From Steve Fassino
- We co-taught Calculus together and you had been teaching that course already. I appreciated how welcome you were to suggestions or changes. I didn’t suggest anything drastic but that openness to allow for me to have a voice made me feel valued. Further whatever I did suggest you often were willing to accept it, which again made me feel valued. Something you also contributed was all of the logistical work of maintaining the Canvas course page for all sections. I know it’s not a huge task but it’s not a non-zero task to make sure it all is working and up to date for all classes.
- I touched on this earlier- so check above. I’d add as a possible suggestion for the improvement question that we didn’t have much collaboration on what we did during class time. We obviously collaborated on assessment design, agreed to a calendar, had the same homeworks, referenced the same course materials (Paul’s Notes). But what we didn’t discuss much was lesson design. And I’m mentioning this only because I like thinking about designing lessons so much as I find it fun to try and sequence problems and questions and activities to help facilitate learning. And so I recognize that might not have been as important of a task to you as it was me so take this with a grain of salt. But to be a better co-teacher in the future, engaging with some lesson design would be something I’d enjoy.
- Well you’re the 2nd longest tenured math teacher now behind me, so we’ve likely collaborated the most together. We certainly did work together on our last scope and sequence (in 2021?). And I recall you’ve done work to collect data and compile data on various little pursuits we had. As the Discipline Lead, I’ve especially appreciated your thoughtfulness and care which you bring to our discipline meetings. While you don’t volunteer to chime in when asked for an opinion you have a well formed one. Whenever you speak you offer something that has merit and should be evaluated. And I appreciate your knowledge of EPS in discussions as well.
I want to add to Steve’s observations that I am now co-teaching with him on Calculus and I have made a point to try to have conversations with him about each lesson we deliver but with only one shared free period, one that he also needs to collaborate for other classes, it has not been as extensive as I would have liked based on his feedback.
From Alicia Iannucci
- This year, you have helped our discipline tie together things we’ve done in the past, so we don’t have to reinvent the wheel and offered your insights and knowledge as someone who has taught our most upper-level math courses. I appreciate that you are always open to new ideas and willing to collaborate on all aspects of our discipline work.
From Brandon Smith
- Extremely supportive, hardworking and open to change. You are always willing to help or support your co-teacher, and also willing to do that small detail based things. Personally, last year, you were invaluable to me trying to get up to speed as I transitioned from a google school to this crazy house of Microsoft products and the monster that is ONE NOTE ‘O doom. Thank you for all that help. You do it quietly and often. This year, I really got to see your work ethic in a classroom. You can PUMP our material, create amazing lessons, build dynamic projects and also put together amazing and extremely comprehensive solution guides. All in all, you are one of the most supportive and willing co-teachers I have had the pleasure of working with. Thank you for helping me get through this difficult year. I wouldn’t have made it without your support.
- We have taken the calculus course and made some positive changes to the kinds of problems we assign, how topics are introduced and the sorts of assessments we give. You have been open to changes all year and willing to innovate and really try new ideas and create some changes that we both think are best practice.
(4) updates course content to reflect the contemporary world
The weird thing about this indicator is how little it understands the modern reality of teaching mathematics at the high school level. The trajectory of mathematics was established somewhere in the early 20th century and has not been updated since. Colleges still expect students follow a linear path culminating in Calculus and look down on any deviation from that path. Yet, I would argue, the important of Calculus as field has diminished greatly since that time. I think that at most Calculus is the third most important field of math we can be teaching, and a distant third at that. The modern world is built on understanding and manipulating large quantities of data and the math curriculum should really reflect that. Not every high school student needs a working knowledge of Calculus or even of Algebra II, but every student should have knowledge of Statistics and a majority need a knowledge of Linear Algebra to handle the modern world. Unfortunately, we are powerless to change this sequence until a major change occurs in the college admissions process, as our main goal is to prepare students for college, which necessarily implies getting them into college in the first place.
That said, I have attempted to implement these subjects into our curriculum where I can. We have our own statistics course and my teaching placement in our sequence means I am often sought out for advice on which math class to take once students get through Calculus (and sometimes before). I always advise students that stats will be useful to them regardless of their future direction in life and will be the most useful math class if they do not want to go into a STEM field. I teach Linear Algebra as the first trimester in Advanced Topics and so will advise students that want to go into computer programming or a STEM field that is not math intensive to go with Advanced Topics over Advanced Calculus if they have to make a choice, although they can always take both. Finally, if they are looking at a math, physics, or math-intensive engineering major, I will recommend they take Advanced Calculus over other math classes.
As both Advanced Calculus and Advanced Topics have only a Calculus pre-requisite, students can choose to take one or the other, or to take both either simultaneously or in different years. I talked about the differences I view in these classes when advising students on which class to take but I also like that Advanced Topics is designed to give students a different view of math than Calculus. So often, students and parents want to engage in the “race to Calculus” and think getting to Calculus is the end of the journey. Advanced Topics allows me to show the students that Calculus is not the end of math and, in fact, math is so much more diverse than what is shown in Calculus. A number of students who elected to take Advanced Topics in addition to or in place of Advanced Calculus have noted how different of a class it feels. There has even been a group of students who have talked about not feeling able to handle the rigors of Advanced Calculus but enjoyed their time in Advanced Topics because of the new and different ways of thinking about math they were exposed to in the class. Moving forward, I would really like to expand the diversity of math we can expose students to, as forcing them into a single track to Calculus strikes me as the most un-EPS thing we are doing at EPS.
Finally, it seems important to mention the integration of technology in the math classroom. Math, just like some many other disciplines, has been bombarded with a range of new tools and given little guidance on how to use them. I find myself agreeing with the stance the school has taken on AI, that it is a tool and our job as educators is to familiarize ourselves with the tool and teach students to use it responsibly and ethically. I apply the same standard to the new tools we are seeing become available in a math classroom. I use 3 Blue 1 Brown videos in all of my classes to help with the visual aspect of math. The creator of these videos, Grant Sanderson, is now a mini-celebrity in my class. I also embrace the use of DESMOS in my classroom and even allow it on tests. I do require students to be in tablet mode or have their computer flat on their desk and I spend a great deal of examinations circulating through the room, checking on their computer usage. I was hoping by now that the DESMOS testing app would be available for Microsoft systems by now, but three years later and they haven’t even got the Android version out of Beta testing yet. Since this system is used on the SAT now, I think it important to give students practice working with it in a testing environment. I also think DESMOS is a good introduction to Computer Algebra Systems and represents a nice first step on the road to learning to use something like Wolfram Alpha or Matlab. Moving forward, I also want to experiment more with the TI-Nspire, which I know has many interesting features that could help facilitate labs and experiments in a math classroom.
Program | Professional Development
(1) participates actively and constructively in Program Development Day activities
My participation in PDD activities essentially boils down to my personality. I try to listen and process the information being given but will only talk if I feel I have something to contribute to the discussion. I typically share my opinions more when we have small group discussions, especially if I am comfortable with the members of my group, than I will during whole school discussions. I will engage in discipline meetings and homegroup talks but the truth is, my main contribution to PDD days are to listen and try to learn. I should try to speak up more but similar to discipline time, what can I potentially offer the wonderful teachers we have here at EPS?
I will typically try to attend the social events that happen during PDDs or after. I have had some physical issues the last couple of years that have prevented me from joining in faculty basketball or volleyball games but I try to play when physically able. I attend the happy hours afterwards and am often one of the last people to actually leave.
Moving forward, I probably need to take a more active role in PDDs, whether that be speaking up more during large meetings or taking on a facilitator role during small group session. I need to be more confident in my role at the school, that my ideas are valuable and can contribute to the school as a whole, and taking on more during a PDD will be a step in the right direction.
(2) presents during Program Development Days and conferences
So far, I have presented once during a PDD and never during a conference. I took part in the project tuning Evolution of Instruction, presenting a project I have been giving to my Advanced Topics students for the last couple of years. Here is the project:
The goal of this project is to lead students to a higher level of thinking about differential equations while also giving them a real-world application in the form of savings accounts, something all the students will eventually have to deal with. I focused the project tuning on the first problem, which concerns savings accounts. The feedback I had gotten from students was split. Many students liked the project and felt it important to their future, but many found the savings account question in particular tedious and repetitive. I can understand that criticism, as much of the question is exploring how things like changing the interest rate, when you start saving, and how much you put in each month will change your savings.
As a result, I was looking for insight into how I can make this project less tedious while still looking at the idea of interest rates and compound interest. I presented to a diverse group of faculty, not just math teachers, and their insights were very useful. Several recommended that instead of retirement accounts, which for our students is a far off proposition, I can do mortgages or student loans. It was even proposed that I make the first question one where students can pick their own path, working on one of retirement, mortgages, or student loans. I really liked this idea and plan to incorporate it into the project next year.
As with every indicator in this category, I know I need to be better moving forward. I need to present more during PDDs and will take a look at the calendar of Evo’s next year with the goal of presenting once during the year. I still don’t think I’m ready to present at a conference outside of EPS but presenting during a PDD should help me be more confident on this front.
(3) takes advantage of professional development provided by the school
Since I was hired here at EPS, I have been to several conferences. The school places the first PDD of the year on the day of the NWIAS conference, which I have attended every year except this year when we instead held discipline retreats. With the rest of the math discipline, I have also attend the NCTM conference in 2018 and 2022. In all honesty, I do not get a lot out of the conference sessions. The NWIAS conferences are small but are highly specific to independent school teaching and so I find that many of the sessions I attend are repetitive of ones I have seen before. The number of sessions that pertain to teaching math at the upper school level can also be limited by the nature of the small size and full education scope of the conference. On the other hand, the NCTM are designed for math teachers, so it is easier to find sessions that pertain to upper school math but even then, it is highly focused on the future of Algebra II and Pre-Calculus, with very little sessions for teaching Calculus and beyond.
That is not to say I do not get anything out of these sessions. I have adapted a full inquiry-based lesson from one of these sessions, introducing students to the concept of optimization by having them design packaging for a twelve pack of soda cans that starts with giving them no additional restrictions and slowly building them up to thinking about the idea of minimizing packaging material. Many of the technology sessions I liked, and I have made efforts to incorporate the things I have learned about DESMOS into my classroom. With a push to require calculators again, I also have seen some interesting things done with the TI-Nspire calculator and want to look into the attachments available for it.
However, what I find the most rewarding about the conferences are the opportunities it allows for connection with my fellow teachers. The NWIAS conference typically ends with a bunch of EPS faculty enjoying a happy hour and reflecting on the conference. During the last NCTM conference, I was able to spend an hour talking with Lurline Sweet, a former EPS teacher, and reconnect. Since the conference was in Tacoma, the school provided hotel rooms and we were able as a discipline to have dinner and socialize. It was so much fun having the time to joke around with my discipline mates and get to know them better. We even got to enjoy some time in an arcade:

Beyond conferences, I have also made an effort to observe my discipline mates teach. So far, I have been able to get into everyone’s classroom with the exception of Adam and Gaylynn and I plan on rectifying that sometime next year. Getting into other teacher’s classrooms has given me some absolutely amazing ideas on how to improve my own classroom practice. Moving forward, I want to make sure I get into at least one math classroom a year and hopefully start getting into the classes of other disciplines. EPS has such a wealth of knowledge when it comes to teaching and one of the ways that I can improve is by tapping into it.
(4) identifies and pursues professional development opportunities appropriate to enhancing effectiveness as an educator
This indicator is something I need to improve on. I have not done any identify of professional development opportunities since I started at EPS. Part of that is the nature of the last couple of years. Between COVID and remote teaching, which started during my second year, finding professional development was very much on the backburner. I started to think about it a little at the start of my fifth year, but I got burned out to the point of almost quitting and it seemed more important to take some time for myself. I was not able to look for professional development last summer as I had jury duty for five weeks. This year, I guess this PDP would count as pursuing professional development, the first real pursuit in my time here at EPS.
Moving forward, I need to search out more professional development. My biggest weakness as a teacher is my lack of knowledge of traditional general teaching practices and classroom management. I need to seek out training in these areas. I also want to find more conversations about the teaching of Calculus and higher level math in the high school level. The conversations I typically see revolve around Algebra II and Pre-Calculus and while I am not uninterested in these conversations, I also need to find conversations around the classes I teach as well. It was mentioned by Jonathan Briggs that observing other schools might be an avenue to explore these sort of higher level classes and I am very interested in trying something like this next year. Maybe we can arrange it so some of their teachers come to observe us as well and try to create a dialogue between the math disciplines of both schools.
Finally, as I mentioned for the last indicator, I want to observe classes from other disciplines. Observing the higher level science courses or even literature classes that cover more abstract concepts might help me learn ways to better convey abstraction in math. Even beyond math, observing other teachers, especially those with a firmer foundation in the class management side of teaching, would help me improve on that front. In truth, I am open to any ideas on professional development I can pursue but I need to get better at seeking out these opportunities as well.