Pedagogical Practice

My classroom style has been shaped by the journey I took to get to EPS.  I come from teaching college but left that level because of the impersonal nature of teaching.  As a result, I have a comfort in teaching in a college style but want to make sure I have great relationships with my students.  I do not have many classroom rules for students to follow, instead relying on the fact that the grade levels I teach, mostly juniors and seniors, are going to be self-motivated to learn.  EPS does a great job of choosing students like that, so it has become a good match.  Part of learning is being in an environment where you are comfortable making mistakes and asking questions, so I try to make sure students know I am invested in their success, both inside and outside the classroom.

I try to follow a couple of core tenets in my class.  The first and most important is that anyone can learn math.  The notion of a “math person” is completely false and also highly damaging, as it ruins confidence levels for students who just need more time to learn the material.  Time will always be a factor in a math classroom, as there is a certain amount of material I must get through to ensure students are prepared for the next class in the sequence, but I try to give as much time as possible in class for students to practice.  It is also important that students do not get discouraged, which means they must be comfortable making mistakes and asking questions.  Part of being comfortable is knowing I am invested in the success of my students as people.  As a result, I try to make myself visible to students outside the classroom, attending their concerts, plays, and sporting events.  I also try to create a fun environment in my class, asking non-math related intro questions so students get comfortable giving silly answers, and joking around with my students during class.  I am always available to students outside of class as well, but expect them to reach out to me when they need something.

My next tenet is that while practice will not make perfect, it will make understanding.  Time in class is always given for students work on problems, whether that be sprinkled throughout the lesson for the day or time to work on homework at the end of class.  Students are free to work in any manner they see fit.  I want to encourage collaboration, so my classes are often loud and a little crazy.  I allow students to work individually as well if they want but need to work on better incorporating quieter students into the groups during this time.  I also allow students to work on whatever medium they find most comfortable, be that whiteboard, laptop, or pen and paper, and also allow students to work in the hallway if they wish.  I do not require memorization, instead endeavoring to get students to a deeper understanding of the material and ideally to a point where they can rederive what they would have memorized on their own if needed. 

Finally, students are expected to take ownership over their own education.  I come from teaching at the college level and give students the kind of autonomy in my class that they would receive at the college level.  I do not police my students.  Instead, I expect my students to be self-motivated to pay attention.  I will not redirect students unless their inattention is getting to be excessive or distracting to others.  Students can choose to do other things during work time but know I expect that time to be repaid outside of class, so if I give twenty minutes in class to work on the assignment and they choose not to, then they need to spend that twenty minutes outside of class on math in addition to the usual 30-45 minutes I expect to be devoted to homework.  I have run into issues with this hands-off philosophy in the past and still need to improve my class management skills, but I have gotten a lot better on this front and think I am getting to the right balance of trusting students while also stepping in when they overly abuse that trust.  I embrace our mantra of a high trust environment and that our job is teach students how to use tools responsibly and ethically, so I trust them in the use of tech in the class.  Tech is permitted to be used at all points during work time and DESMOS is even allowed on tests, provided their laptops are either flat on their desk or in tablet mode.

Classroom Culture

(1) coaches and reinforces peer-to-peer dynamics that are appropriate and constructive

(2) communicates behavioral expectations that are appropriate to class activities

I am going to lump indicators (1) and (2) here into the same statement.  It seems to me that it will be easier to talk about behavioral expectations in my class as a whole than to divide it into peer-to-peer and individual components, as I find them intertwined.

My philosophy in the classroom is designed to alleviate two concerns while promoting learning.  The first is that math anxiety is real thing and a major impediment to learning.  The second is that seventy minutes is a long time to pay attention, especially to something that does not interest you.  My goal therefore is to create an environment in class where students are comfortable playing with mathematical ideas while allowing them the avenue to be distracted by five minutes if they need to be.  I have often described my classroom as organized chaos, where students are free to play with math and make mistakes but also free to make jokes and spend five minutes talking about their lives with their peers or with me.

My classroom is structure similar to a collegiate style, but with more dedicated time to practice and collaboration.  Since I teach mostly juniors and seniors, I try to treat my students like adults.    That means students are expected to take ownership of their own learning.  I do not intervene when students are not paying attention unless it becomes excessive or it distracts the rest of the class.  Instead, I take the approach that students are responsible for their time and if they do not pay attention, then it is their responsibility to catch up to the rest of the class.  This is most notable when I give students time to work on their homework in class.  I tell the students that this time counts as part of their homework time, which I try to limit to 45 minutes outside class.  If I give them 20 minutes in class and students do other things during that time, then they are responsible for 65 minutes outside of class.  The choice of how to spend their time is the students to make but the expectation on how much time is spent is known.

In my mind, math is a collaborative exercise.  As a result, I encourage students to talk in my class.  I want them up at the board with their peers or talking to their neighbors about the problems.  I let the students arrange the tables in any manner they see fit and there are no assigned seats.  Students have the freedom to arrange themselves as they like and for the most part, can work with who they want.  This is also reflective of my background coming from college.  Here are some photos of the students in action:

To illustrate the environment in my classroom, I offer the following observations:

From Jonathan Briggs:

• The class environment is relaxed and presumes that students, when presented with a challenging puzzle, will be driven to figure it out. This allows for an intrinsic desire to solve problem to grow within the students. There is no hint of elitism or building of math egos, just a collaborative exploratory environment.  Humor is evident throughout the experience. Students feel free to make small jokes as does John. All jokes are appropriate and playful.
• Like other classes, friendly, informal atmosphere but with high level math going on. Students seem to be tracking concepts well, getting right to work when demo problems are up on the board.

From Ian Corey-Boulet

• mood in the class is calm and focused; students are using the time well
• teaching presence is very calm and reassuring, which I imagine is a great help, given the difficulty of the material

From Molly Lori

• Was able to joke with students about their answers – you can tell he has a good relationship with them.
• Students were able to ask questions on their own.
• Students were able to talk at their tables and help each other.
• They call him ‘Kaminsky’

One change I have made to class this year and I would like to continue moving forward is how I approach testing and grading.  I have moved to a system of handing back tests with mistakes highlighted and no grade.  The grade is in canvas along with a breakdown of the grading system but those remain muted until after the class.  Students then correct their tests and are allowed to collaborate with their neighbors in the corrections.  This allows students to acknowledge their mistakes to their peers and help encourage students to treat these interactions not as a sign of their inadequacy but a place for them to seek help and guidance without judgement.  As one student put it, this is an opportunity for growth.

That is not to say I am perfect on this front, as I actually feel this is my greatest weakness as a teacher.  Classroom management was not something I had to worry about teaching college, and I do not have the background in it that properly trained high school teachers do.  One thing I do know is I do not want to lose the comfort and fun my classrooms possess but I definitely can be too lenient at times.  I will rein students in, but my leash was way too long when I first started.  I think I am getting better on this front, as Anne Duffy noted:

“This hasn’t come up as a topic of conversation in the last couple of years but I know that there have been incidents related to classroom management that could have been handled better. That being said, I really think that the kids like that you treat them like adults and that you don’t have a lot of “teacher rules and processes.” It seems like you have reach a nice balance in the last couple of years of maintaining that freedom for the kids without them taking advantage of it.”

Molly Lori echoed this sentiment:

“I have this same problem: Students can take advantage of your kindness and abuse their freedoms in class. You can be too laid back at times. Is that a bad thing? (Not sure how we can suddenly become stricter…)”

I also need to be better on making sure quieter students are engaging with the class.  I identify as an introvert who very much wanted to work alone as a high schooler, so I want to give students that opportunity if they want.  However, graduate school gave me an appreciation of how important collaboration is and I need to build in more opportunity for these students to contribute. 

(3) develops a mutually respectful relationship with each student, instilling confidence that the teacher is invested in their success

My main reason for making the transition to high school education from college was a chance to have better relationships with my students.  Teaching in college left no room to get to know my students, as they become just faces in the crowd and numbers on a spreadsheet.  Teaching at the high school level means getting to know students on a personal level, learning their interests and goals and helping them grow as people.  My favorite part of this job is not teaching math; it is the relationships I have with my students, the times they joke with me or invite me to watch their sports games, plays, or concerts.  Students know that I want them to not only succeed in my class but also become awesome people.

No better evidence for this can be had but from the students themselves:

You can find some other notes from students in the Relational Cultivation section as well as the next indicator.

And from class observations by Ian Corey Boulet and Molly Lori:

• before class, Cooper says “you’re the dream math teacher”
• Jacob C. – Said he likes the class

Molly also recorded the following interactions with students in the hallway:

First teacher that made me love math! -anna and grace

We’re besties, he wrote a letter of rec for me – Josie

Me too! -syon

These connections have continued as I have alumni reaching out to me for advice on research they are doing or what math classes to take in college, as shown:

(4) demonstrates cultural competence by promoting inclusivity

Math is a subject that often comes with anxiety.  Students often believe in the idea of a “math person,” that math is either something you are born able to do or born not able to do.  I reject this notion completely.  I truly believe that math can be learned and does not require any inherent talent, just a curiosity and a desire to learn.  My classroom is designed to reflect this belief.  I want students actively engaging with the material in an environment where making mistakes is not only allowed but encouraged as an important part of the learning process.  Students do not compete with their neighbors to answer questions faster or do better on tests but instead collaborate and support their peers, recognizing that being able to explain concepts not only benefits the class but themselves.  Within the constraints of having to get through a certain amount of material in order for students to be ready for the next class, as much time as possible is given for students to actively engage with the material and practice their skills.

I have spoken about how I get students to be comfortable in my class in other indicators and how much practice I give.  Instead, I want to focus this indicator on a couple of other things.  One thing I want to talk about, especially in regard to how my class handles neurodiversity, is the flexibility I afford students.  I generally allow students to get extensions on assignments or tests with no questions asked.  I do not dock students points if they hand in homework late.  In my mind, getting the work done is important but the real punishment for handing in assignments late is falling behind in the class.  As I have mentioned before, I expect students to take ownership of their learning and so I will not slow the class down for students not paying attention.  I will gladly support these students in other ways, as my door is always open during my free periods or office hours, but it then becomes a place where they need to take the initiative.  Tests can be extended, and I allow students in GSH to take their tests during their GSH period.  Math tests are high anxiety and anything I can do to alleviate that anxiety without compromising the integrity of the test I will allow.

Support is always available to my students if they ask.  Some peer observations about me supporting students:

From Molly Lori

• You seem to really care about students and you see them. They feel comfortable teasing you but also asking you for help.
• I know that you are flexible and understanding about students with accommodations and try to meet them where they are at.

From Adrienne Behrmann

• You seem to have a great rapport with students and from the feedback I received, students really respect you and find you approachable and knowledgeable in your subject. You also seem to have a great relationship with students outside the classroom.
• You always make time to meet with students when they need extra help. You are compassionate and kind and make accommodations for students when needed. Your progress report comments reflect how well you understand each student and you offered good.

From Sarah Aguiar

• Students engage with you. They trust your and seek your expertise in math (and life)

From Steve Fassino

• Since you’ve been here I’d say this has always been a big asset of yours. You’ve always done well to cultivate a playful silliness and sarcasm in your classes that builds relationships. Also I’ve noticed that you tend to show up to your classes about 10 minutes early – so you capitalize on that unplanned time to build relationships by joking around and connecting. In recent years it seems like students seem more comfortable to approach you outside of class, but that’s just my sense of things as I don’t have any concrete evidence.
• In one-on-one meetings with students, you have a willingness to wait non-judgmentally as students are wrestling through something that is admirable. By not jumping in right away and coaxing them to fit the pieces together you’re supporting them. In how you write a fully copy of the class notes and have full solutions to homework, I think you’re supporting students by providing those detailed resources.

From Brandon Smith

• It is hilarious how you try and make them think you don’t like them. When in fact it is your time with them that brings you the most professional joy and fulfillment. We forget sometimes, in our rush to do all the adult things of an institution that it really should always just be about the kids. You let you kids be kids, you support them and stand up for the ones that are viewed with a (potentially unfair) critical eye. John, you and an advocate for their learning and also for making their experience authentic but also extremely rigorous. Youd don’t ever compromise that. I think they appreciate how much you challenge them and look up to you as a mentor in this great field.
• With the lessons you create… trying everyday to give them authentic learning tasks and cutting things that are busy work. You show your support in all of the solution guides you make, in the speed of grading a feedback and simply in the way you speak with them, but also in the way you speak about them. You speak of your kids with an level of appreciation, understanding and compassion. You are understanding first and judgmental third… and this is a long while and may attempts at support in between.

The best compliments I ever receive from students is not when they say I am a good teacher or even that they enjoy my class.  The best ones are when students say they found something new in my class and that led them to either start to love math or rediscover their love of math.  I will highlight a couple of these below

In the bottom on the right page is a note from Ayezah Dar.  It is hard to read but the note is about how much she came to love math being in my class.  I want to start with this note because I bumped into Ayezah during the special 20th anniversary fall harvest and she told me she was declaring herself a math major, in part due to her love of my class.

A couple of others:

From Molly Lori’s observations:

First teacher that made me love math! -anna and grace

(5) designs and facilitates a classroom culture that promotes student preparedness, engagement, self-advocacy, perseverance, and collaboration

This indicator describes my class well as I envision it running.  My classroom is designed to reduce math anxiety and increase student engagement.  I use humor to help students feel comfortable and encourage students to be silly, provided it does not go overboard.  I also ensure that I am visible at school events so students know I am not just their math teacher but someone who is invested in their success in life.  These two things make students comfortable in my classroom and with me as their teacher.  My hope is it leads to students being more willing to make mistakes around me.  A big joke in my class is that I am constantly judging students, but it is important to me is that students know I am not judging them as a person when they make a math mistake but merely correcting and shaping their math skills.  I only judge them as people when they do something actually stupid, like invite me to their Super Bowl party or stick a tin foil gum wrapper into an electrical outlet as a senior (both these things have happened to me).

Coming from teaching in college, I place a large onus on the students to be responsible for their own learning.  Students are expected to be prepared for class, to take ownership of their own time management and to reach out when they need support.  Practicing math is student choice.  They have options to work individually or collaboratively, work on the whiteboard or at their desk, or even leave the classroom to work in the hallway.  During this time, I am constantly circulating throughout the class and will pop out to the hallway if I have students out there.  I have certain students I know to check in with during this time but for the most part, I rely on the students to ask questions rather than initiate the conversation.  This follows my principle of support is available if you only ask.  This extends outside the classroom as well, as I will always find time to meet with a student if they ask.  Similar support is available for tests, as students can generally receive an extension if they ask and GSH students have the option of taking tests during their GSH period.

Considering this is the last indicator in this section I am writing, I feel like I addressed a great deal of this in other indicators.  I saved this section for last not only because it ties together the other indicators but I feel like this is a great place to give all my class observations as evidence.  These contain not just the great things about my class, which I have sprinkled throughout this section as evidence, but some of the warts as well.  As this indicator was described by my facilitator Sarah as my big theme, I thought it the right place to place my classroom on display as seen through the eyes of my committee.  I believe these comments illustrate not only what make my classroom a great place to learn but also where I still need to improve.

 Sarah Aguiar, 10/26/23

Jonathan Briggs, 10/27/2023

Ian Corey-Boulet, 11/3/2023

Molly Lori 11/7/23

Jonathan Briggs 1/30/24

Molly Lori 2/14/24

Pedagogical Effectiveness

(1) begins class sessions with a clear statement about the lesson’s objectives and place in the progression of course

For each class, there is an agenda.  For example, here is a sample agenda for Advanced Topics:

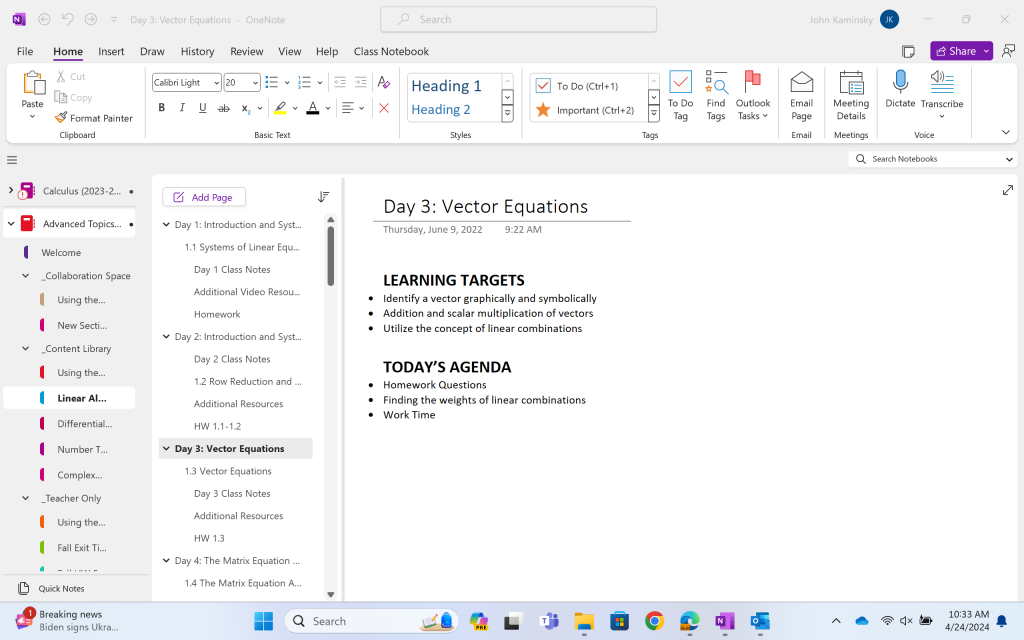
I give a screenshot of the entire OneNote page as it gives a glimpse of my OneNote organization as well.  I prefer tabs to single pages.  Each class period is listed with the day in the trimester of class, a title of what we are studying that day, and the learning targets and agenda for that day.  The next page down, indented to the right, are the textbook reference for that day.  Additional resources with links to outside support and the homework are additional tabs.  After class, the notes from the day are included in the tab as well.  This should also be posted well ahead of time, as everything from agenda to homework is posted at the same time and I generally obey the rule about posting homework the week before.

That being said, I do not usually project or display the agenda at the start of class.  It is in OneNote for the students that want them, but I find actually displaying less important than answering student questions as they walk in, getting solutions distributed, and having the introductory things ready to go.  I have been told to have the agenda displayed throughout the entire class but that never made sense to me.  Displaying it throughout the class takes up valuable whiteboard real estate and I want to utilize that space for either class content or student work.  I also want to prepare students for college, where the agenda for the entire course is given in the syllabus rather than day to day.

As for making sure the students know where this class is in the progression of the course, that flows naturally in a math class.  Math inherently is building upon itself, so I am constantly referencing material we have covered previously or giving glimpses of where we are going.  Class starts with homework review which then transitions into the new concept for that day, which is often expanding upon the concept review in the homework or demonstrating a new technique for that concept.  Hard pivots sometimes happen but are typically done after a test or at the start of the next trimester, allowing students to use these as guideposts for when the class might change direction.

(2) designs and implements varied activities in each class period

To be honest, this is something I have struggled with.  My time teaching college mostly involved large lectures, which limits the amount of innovation and variety you can have.  Thus, when I was hired at EPS, my class was very repetitive.  Even as I have gotten more comfortable teaching high school and incorporating new things into my class, I still have stuck to a basic structure.  I do think there is something to be said for having something like that, especially in math, as students know what to expect in class and that can help reduce anxiety.  Finding the right balance for me is the main challenge, as I want students to know what to expect in my class without feeling bored by doing the same thing over and over.

Steve Fassino noted this as well:

“Again mentioned in the co-teaching question, and I don’t know if this is something you want to focus on so disregard it if not a priority. But I think your lesson design could be more varied. Granted you often teach the students who are closest to being enrolled in college and therefore should be having similarly academic experiences. And I think sprinkling in some varied activities and more inquiry every so often might mix up which students you’re connecting and engaging with.”

As did Brandon Smith:

“Never change your amazing work ethic. That is such a tool that seldom is considered when people want to enact change. You can JUST DO THE WORK AND MAKE CHANGES… debate over. I would challenge you Jon to continue to innovate. Ask yourself why we do things, and can we do that better. This is easier to do when you have other around and it is a conversation, but needs to be more intentional if you are working by yourself. You work at the top of the tower bud… Topics< Adv. Calc… etc. Set yourself a goal to make an intentional change to your practice all the time… problem sets, projects, labs, assessments, anything you can do… take a moment to reflect why and try new stuff. You are a talented teacher, John. Good luck :)”

The structure that I find works best breaks down the class as follows.  The first five to ten minutes are an intro question, homework review and some kind of warmup activity.  These are meant to get students comfortable and ready for the class while also making sure the last class is fresh in their mind.  The next forty to forty-five minutes is the actual lesson for the day.  The actual lesson will depend on the material for the day and can feature some direct instruction and some inquiry but will also feature some kind of work time for students to practice.  Whatever time remains between when the lesson finishes and the last ten minutes of class is time for the class to get started on the homework, allowing for more practice time on the material with me in the room to answer questions.  The last ten minutes are for an exit ticket, enabling me to get a gauge on the class’s understanding for that day.  The problem should only take five minutes but ten are given so students with accommodations do not have to worry about using the break between classes to finish.

In terms of the presentation of new material, there is a good amount of direct instruction involved.  I will show a technique or concept on the board, work through a problem with the students, and then let them practice that concept on their own for a bit before reviewing their work.  I will attempt some inquiry in this time, with questions guiding students to a certain concept, if I feel that the majority of students can reasonably reach the conclusion within the given time frame.  I would love to do this more, but time is always a factor, as I know what I need to get through not just each day but at the end of the year to prepare students for the next class.  To counter this problem somewhat, we introduced labs this year in Calculus.  These are often done before major topics as a way to introduce students to the concept in an inquiry style.  For example, to introduce the idea of Riemann Sums this trimester, we had students come up with their own way of approximating area under curves in a lab.  This allowed them to work on the idea on their own and come to the idea of using rectangles and triangles as the best shapes to approximate the area.

No problem is given in class or in homework without a solution being provided at some point for students to check their work.  I type up all my lesson plans and post them to OneNote by the next class period.  Solutions to the homework are distributed at the beginning of class.  Support is always available to the students as well.  Students are free to work on problems in any manner they deem fit, whether that be in groups or individually.  Work time is fully individual, and I try not to police students and what they are doing, instead trusting them to know what needs to take priority and get their work done.  Textbook references and supplemental resources for every topic are included in OneNote for students to peruse as needed.  The supplemental resources include not just written out problems and solutions but links to Kahn Academy and 3 Blue 1 Brown videos for students who want a more dynamic experience.

I have incorporated some variety into classes when possible.  Students love to use DESMOS and I try to allow that as much as possible.  When reviewing concepts, I try to find or create DESMOS activities to practice, and students are allowed to use the graphing calculator function on all their assessments.  Molly Lori observed one class where I use a DESMOS activity, observing that I noted “today is our last day of material. We’re reviewing. There’s a DESMOS activity for today. The link is in OneNote for you. The homework for today is to finish the DESMOS activity. Match functions to their derivatives.“  Instead of forcing students to memorize concepts, I try to use Kahoots to help students with things like the unit circle and derivative formulas.  Every major assessment, whether it be a project or test, gets at least one day in class to either work on the project or review for the test.  The projects often help students see the application of math to the outside world and having that time in class gives them a chance to ask questions and check their work with me.

One new thing I incorporated in class this year was test corrections being done in class.  This has led to some great discussions amongst the students, especially since they do not know their score and only know what they did wrong.  Molly noted from the same class:

Test corrections: Great way for students to actually look at their work! And learn from it.

Walked around helping individuals with their tests from last weeks. Test answer corrections.

Students were able to talk at their tables and help each other (GREAT)

(3) brings each activity to closure effectively and transitions intentionally to subsequent activities

Since I mostly teach juniors and seniors, I tend to not emphasize the closure of an activity.  Junior and Senior students tend to not need a lot of redirection, so simply calling out is usually enough to get them back on task.  Occasionally, I will need to make a second announcement and under the direst of circumstances, staring at them until they are quiet and dropping a “Are you done?” is enough to fully shame them.

Class usually begins with an intro question that is more fun and not math related.  Students generally look forward to this question, so it is not that hard to get their attention.  Class then transitions into homework questions and a warmup.  Again, this is usually a quick activity, so students basically have time to review their homework, ask questions, and get the warmup done.  Even if they do not get to the warmup, students know it is more review of the material from last class, so reviewing the homework can also suffice.  We then transition to the material for the day, followed by the homework.

The main issue I struggle with here is trying to balance giving enough time for the slower students to finish the assignments while ensuring the faster students are not bored.  To that end, I give students a lot of autonomy since they are about to go off to college and should be able to handle their own time management.  If they finish the assignment quickly, they can get started on the homework or do work for other classes as needed, provided they are not disruptive to the rest of the class.  I make a point of checking in with the slower students and giving them the option of telling me if they need some more time to work on the problem.  They can also choose to stop where they are and follow along as we go through it.  This is noted by Ian Corey-Boulet during one of his observations:

• asks if students need more time, a couple of them request it; he notes that the others can and should get started on the homework, because it’s longer
• goes around the classroom and checks in with students who are still working
• runs through the example on the board

The end of the class consists of work time.  This allows students the time to work on the material covered in class while also having access to me to ask questions if needed.  Review classes and other special classes like lab periods also end in this manner, stemming again from my belief that math is best done by doing.  Some classes such as Advanced Topics may also have an exit ticket at the end of class.  Together, this helps wrap up class, as students practice on the material leading directly into the homework. It also ensures I do not go over my allotted class time or try to rush a concept at the end of class, issues I had when I first started at EPS before I got the rhythm of our class time down.

(4) ensures that students are using technological tools effectively

I consider technology essential to a math classroom.  Getting a Ph.D. in mathematics gave me a sense of where math shows up in the real world and in nearly all these instances, some kind of technology is utilized in concert with math, whether that be as simple as a four-function calculator or as advanced as running simulations on quantum computers.  I want students to get comfortable with this technology, so I allow these tools to be used in the classroom at all points.

The most popular piece of tech students may use is DESMOS.  Students love the graphing feature, and the calculator is convenient.  I consistently see students fire up DESMOS when starting a problem, a move which I applaud.  Students are allowed to use this on tests as well, but to ensure that they aren’t utilizing additional resources, students must lay their computers flat on their desk or have it in tablet mode.  This way, as I circulate throughout the classroom during the test, I can ensure the students are only using DESMOS.  Visualization is important in math and tech has made this aspect some much better.  Beyond DESMOS, the great amount of math videos on the internet, a number of which have some excellent visualizations, has made giving students the visual of what the math is doing so much simpler.  I especially like to use 3 Blue 1 Brown videos in class.

Students are allowed to use other pieces of tech as well.  Graphing calculators, though not required anymore, are permitted for students to use, as are the calculators that come built in on phones.  An interesting use of technology showed up on the last Advanced Topics exam I gave.  The test was on Number Theory and I had an out of class portion where students had to decrypt a message.  They were free to use any software they wished to decrypt the message and a number found a nice online program that would analyze the decryption process to give the most likely message.  Others use their programming knowledge to write a decryption script.  I thought this was a very effective use of technology to supplement a test and the kids seemed to enjoy it (although that might be more because I encrypted random songs for their messages).

For the most part, I rely on the students to use the technology responsibly.  I have to do very little teaching on the technology, as students are usually comfortable from prior classes.  Most of what I do then is showing them a new technique they did not know the tech could do, but the students tend to pick these up quickly.  I do not police the tech use in the class all that much.  This again goes to the idea of teaching juniors and seniors, students who are about to go to college where they will have to be responsible for their own attention in class.  If a student is being egregiously off task, I will give them a reminder to do their work but usually just circulating throughout the class is enough to get the students back on task.

Finally, it is important for students to realize this technology is a tool.  This means that it is important that students understand what exactly the tool is used for and why it works.  Students often ask me why we are learning something to do something when their calculator can do it for them.  My response is to tell them that it is important to know how and why a calculator does what it does and why the answer it gives you is correct.  A calculator is just a brick if you don’t know why it works and is completely useless if you don’t know if the answer you get is reasonable.  Therefore, my class is designed to value that deeper understanding and critical thinking over rote problem solving and memorization.

(5) concludes class with a summary and clear tie-in to the next class

My preferred way of ending class is through an exit ticket.  Exit ticket give students a single, relatively simple problem related to the material covered that day.  It is supposed to be done in five minutes, although I give ten minutes to account for student accommodations.  Students are allowed to work collaboratively on this problem.  The main goal for me is to judge whether students are understanding the material for that day.  Provided most, if not all, of the students get the question correct, then it is a sign to me that they followed the material somewhat from that day.  A number of students getting the question wrong for anything more than just a sign error tells me I need to slow down or redo the material the next day.  Coupling an exit ticket with a quick glance at the homework will generally give me an idea of what students are missing and I can adjust accordingly.

I do not end with my class with a summary, per say, or a direct idea of what we are going to do next class.  Most of my classes involve either a new technique or concept, building upon what was done before.  Class ends with time to work on that new piece of material, practicing it to ensure understanding on the road to mastery.  Since math is constantly building upon itself, my class does not end with a summary so much as it features a review in the beginning.  Class begins with checking homework solutions and a warmup that usually is related to what was learned the prior class.  The next topic should then build upon what was done last class.

That is not to say that I do not give students insight into future topics.  I am constantly referencing when students will see this material again, not only in the current class, but in future math classes.  I have taught Pre-Calculus, Calculus, Advanced Calculus, and Advanced Topics in my time here at EPS and so I know what topics will show up in these courses.  In addition, I came to EPS from teaching math in college.  This gives me the knowledge of when the material we are learning will show up again and I try to pass that on to the students.  This was observed by several members of my committee:

From Sarah Aguiar

• Reviewed prior knowledge
• Connected prior knowledge to new learning
• Connecting HW to prior math experience.

From Jonathan Briggs:

Students clearly see connection to prior concepts, “this is like recycling last trimester’s eigenvectors.

From Steve Fassino:

• “Do you remember the chain rule from last year?  Well now we will reframe it in terms of the integral.”

I also want to give a quote from Eric Zhou, an EPS alumni who I bumped into at the airport this winter: “All the topics we covered in Advanced Topics were exactly what we did my first year in college.”

One thing I am trying to improve upon this year is expanding those connections I emphasize in class to include other disciplines as well.  In Advanced Topics this year, I have made a point to have at least one question on each test be related to some other academic field of study and to vary that up.  David Lao was kind enough to review a chemistry problem I wrote for the first test and moving forward, I want to connect with more teachers here to include more problems like this, not just in Advanced Topics, but in all the classes I teach.  The one issue with this is math not being taught in grade levels, as I need to ensure that if I do write these kind of extension questions, then they are doable by everyone in the class.  This means I need to have working knowledge of what grade my students are in and what classes they have and are taking.

Differentiated Instruction & Assessment

(1) considers and addresses each student’s learning profile

I came to Eastside Prep after teaching in college, so my style is very much a collegiate one, which I think works well as I mostly teach junior and senior level classes.  I let students take ownership of their own learning, as they should know their own strengths and weaknesses by now.  The students are given the responsibility of deciding how to spend their time in class, as I do not “police” my classes.  In college, students are responsible for their own attention and notetaking.  My class helps prepare them for that experience.

That is not to say that I just leave student learning to them.  I build in numerous guardrails to help the students.  All my class notes are typed up and placed into OneNote, along with additional resources for support.  Homework solutions are typed and distributed to the students to review.  Time is given in every class for students to work on problems and ask me questions.  Students are free to choose the manner in which they work, whether that be in groups or individually, and I also allow students to work in the hallway if they prefer.  Homework must be submitted electronically but can be done in OneNote, using pen and paper, or on the white board.  Tests can be rescheduled if needed and GSH students are allowed to take tests during their GSH period.

One of the hallmarks of my classroom is that it is welcoming.  Math often breeds anxiety amongst the students, which can lead to discouragement and the idea that “I am not a math person.”  I reject the idea of a math person and seek to help every student come to appreciate their own mathematical talents.  However, I also recognize that while everyone can learn math, not everyone will love it in the same way I do.  I am always trying to find ways to connect math to my students’ interests, and that means I need to know my students’ interests.

The welcoming nature of my classroom has been noted by students and outside observers:

• The class environment is relaxed and presumes that students, when presented with a challenging puzzle, will be driven to figure it out. This allows for an intrinsic desire to solve problem to grow within the students. There is no hint of elitism or building of math egos, just a collaborative exploratory environment.  Humor is evident throughout the experience. Students feel free to make small jokes as does John. All jokes are appropriate and playful. – Jonathan Briggs class observation
• mood in the class is calm and focused; students are using the time well – Ian Corey-Boulet class observation
• Was able to joke with students about their answers – you can tell he has a good relationship with them.  Students were able to ask questions on their own – that’s safe. Others got off task at the tables. – Molly Lori class observation

It has also been noted by students in my experience surveys.  Here are a sample of responses to the thing I would most compliment my teacher on:

• He is really knowledgeable of everything he is teaching and he keeps and really light classroom environment which is nice because some math classes get a really dull vibe. 
• His ability to make everyone feel comfortable when sharing their ideas.
• Making class fun
• He makes the classroom SO much fun but surprisingly productive.
• we can be both having fun and productive somehow at the same time?
• He makes class fun with a good sense of humor and can explain things in a different way if I didn’t understand it earlier.
• My top compliment would probably be the way he teaches. Everything is very clear and understandable and we always get time to try it ourselves and ask questions if we don’t understand.

Some other comments from students on other questions in that survey:

• My favorite project activity was the puzzle day because it helped us rewind while still being educational and helping us think.
• the teaching presentation at the end of fall tri
• The classroom experience, the ambiance and the chairs and the overall aura really contributed to my overall experience that I had while I was in this class.
• it really helps me have time to fully go over the material and i feel like i learn a lot because i get to collaborate with my peers and ask the teacher for help.
• Math was made applicable to real world

All that being said, I did think I have some room for growth here.  My style, by placing more of the onus for paying attention on students, naturally leads to distracted students.  This can lead to class disruptions, and it has been noted by some students in my survey responses that I can be too lenient with students.  I am still working on finding the ideal balance, although I am better at it now than I was when I started.

(2) designs class activities and assignments that engage and accommodate for both individual students and a diverse group of learners

One of the main tenets of my class is that doing math teaches you better than listening to math.  Therefore, every class has some time built in for students to practice on the material for that time.  This time allows students to “get their hands dirty” with the math, so to speak, and is sprinkled throughout the class.  This can take different forms during the presentation of new material.  Sometimes, it can be students building the intuition for their new material via inquiry. 

Here is an example:

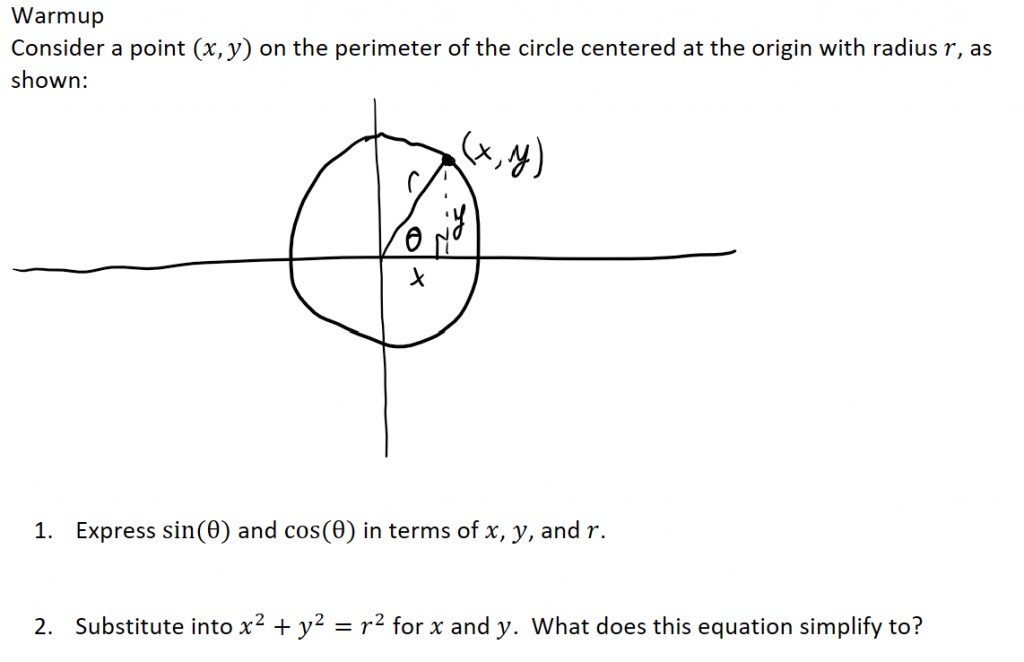
This is a problem given at the beginning of class in Pre-Calculus for students to work on.  The ultimate goal is for them to derive the identity

on their own.

Other times, students are practicing a technique I have just shown to the class.  My goal in class is to limit this instructional time to about 45 to 50 minutes of the 70 minute class time.  Depending on whether I give exit tickets in that class, that leaves 15 to 20 minutes in class for students to get started on the homework.  Students are free to choose how they interact with material, whether that be working independently or in small groups.  To illustrate this, I offer the following observations:

From Sarah Aguiar

• Inquiry question to start class.
• Gave students time in class to work on HW.
• Students work together on homework and classwork problems
• Students have a conversation about number theory and cryptography.

From Ian Corey-Boulet

• provides an example and asks for solution; Arjun (!) volunteers and is correct
• then presents a more complex example and notes that the notation is tricky; asks a student to help him solve it, and she’s correct
• explains the example further, checks in with students for understanding
• then presents several more challenging problems, re: concepts that they haven’t covered before: “what if you have more functions nested within themselves? … a function within a function within a function?”
• student notes that you have to keep doing chain rule
• walks them through it, pointing out that you have to work from the outside in

As I have gotten more comfortable teaching at the high school level, I have tried to introduce more varied activities and class structures.  After seeing how comfortable students have become with DESMOS, I have tried to incorporate it into my class as much as possible and allow the students to use it on all their work, including tests.

I have experimented with Kahoot games in my class.  These can be useful but are material dependent.  They work well when it comes to formulas and easier computations but are not useful for the more complex computations.  I have also had mixed results from students, as some students love Kahoots, especially those who can process information faster, while some dislike them.  Having one or two a year can help give the class a nice changeup.

One outside resource I have come to really appreciate and try to incorporate into my class as much as possible are 3 Blue 1 Brown videos.  These videos are done by Grant Sanderson and have the ability to give a visual intuition to mathematical problems that I can’t match drawing by hand.  Students seem to love these videos and even though some can be as long as 20 minutes, very rarely do I see an inattentive student I show them.  They can even keep my attention, even on the third or fourth time showing it.  Sarah Aguiar in her observation of my class noted that this was the one time I had every student engaged.

Finally, I am trying to expand the number of projects that occur in my classes.  In Calculus this year, we introduced “labs,” which are really just in class projects designed to introduce students to a new concept and then write a report about what they learned.  Labs have included timing matchbox cars down a ramp to estimate speed, calculating the derivative of a function at several points to get an idea of the derivative function, building boxes from pieces of paper to see the various volumes that can be created with the goal of finding the maximum, and estimating the area underneath curves by using easier shapes.  Here are some photos of the students in action on the matchbox car lab:

(3) builds in opportunities for each student to contribute during each class period

There are many ways students can contribute to my class.  One of my big beliefs about math is that students learn math by doing, not by listening.  Therefore, I try to build in time in each class for students to work on the math directly.  This can take several different forms in my class.  I also try to create opportunities for students to get comfortable contributing in my class.

A typical class period follows a certain structure.  It begins with an into question before we get started on the material for that day.  These questions are designed to be silly and help the students feel more comfortable in class.  I started asking them in class during the pandemic and students seem to really enjoy them.  It is hard to come up with new questions every day, especially when I teach the same students for two or more years.  Examples of the type of questions I ask can be found in peer observations:

From Sarah Aguiar:

• Inquiry question to start class
• Question comes from Sam Allen – Who is going out first in the Hunger Games?

From Molly Lori:

Attendance question:

Pick two fictional characters to be your parents.

-Snoopy and Woodstock. Or Snoopy could be a single dad

-The Addams Family

From Ian Corey-Boulet:

• asks “who wants to lead us off with an intro question?” (best Thanksgiving food)

I try to get every student to answer the attendance question, so everyone at least contributes to this part of the class.  It even got me a shoutout in a graduation speech a couple of years ago (thanks again AJ Held).

Class then typically transitions to homework review.  This looks different depending on the class, but I want to make sure if anyone has questions on the homework, it is answered.  For Pre-Calculus and Calculus, I distribute solutions for the students to review while I walk around to see if anyone has questions.  Students this year in Calculus also have the opportunity to write up their solutions to homework problems on the board.  Advanced Topics typically have more abstract problems in the homework, so there are always questions and I review directly with the class.

We then begin the material for the day.  While some aspect of this is me lecturing, I try to build into each class time for the students to work on problems.  During this work time, students are free to work in any manner they choose.  Some students want to work collaboratively with their neighbors whereas others want to work on the problems individually.  Some work on paper, some on their computer, and some on the whiteboard.  I am fine with all of these, and I am circulating throughout the classroom during this time to check on student progress and help out where I can.  Here are a couple of peer observations about this time:

From Sarah Aguiar

• Gives students opportunities to ask questions for clarification throughout.
• Students work together on HW and classwork problems
• On an example problem I gave:
  • T writes problem on whiteboard
  • 4 students jump into solving problem on whiteboard
  • 5 students writing out problem in notes
  • T reviews the problem with class.

From Ian Corey-Boulet

• asks, generally, if there were any questions about the homework
• Miles says he was confused about 1f
• demonstrates it on the board (chain rule), students take notes and seem to understand
• no more questions, so transitions into talking about the chain rule
• observes that so far they’ve looked at relatively straightforward examples (reviews what these were), and now they’re moving on the more complicated examples — although they still follow the same pattern
• provides an example and asks for solution; Arjun (!) volunteers and is correct
• then presents a more complex example and notes that the notation is tricky; asks a student to help him solve it, and she’s correct
• explains the example further, checks in with students for understanding

From Jonathan Briggs

Student working in a variety of different ways, three on the white board, one on paper, three on OneNote @ table 1

Some watching other solve. Some quiet discussion.

John, walks around getting a sense of student’s pace through the problem.

From Molly Lori

John walks around to help students. They help each other too.

Ideally, we finish the material for the class with about 20-25 minutes remaining in class.  That leaves time for working in the homework in class.  This is done in the same way as when I give an example program in class.  To illustrate this, here is a photo from my Advanced Topics class of the students working on homework:

You can see the various ways students are working in this photo, some in groups and some individually and then some at the whiteboard and some at their desks with their computer or pen and paper.

(4) provides alternative explanations of course concepts

Having a Ph.D. in math does not necessarily make me a good teacher but it does give me an overarching view of math that others may not possess.  I have seen quite far down the rabbit hole, so to speak, and know a great deal about the connections math has not only within itself but to other disciplines as well.  This gives me the ability not just to explain course concepts in different ways and give alternative methods to solve problems but also show how the concepts we learn apply to the real world.

One of the core tenets of my class is that there is no one right way to do things.  There are various ways to think about the concepts covered in a math class, whether that be algebraically, graphically, abstractly, or some other way I am not thinking of right now.  No one way is superior to the other and in fact, each informs the others in certain ways.  It is my job to present each of these ways to the students and demonstrate the connections between them.  To that end, the presentation of material is varied in my class.  The whiteboard or OneNote is used to present the material algebraically, allowing students to either get up to whiteboard or copy over to OneNote to work on the expressions themselves.  Images and videos are used to demonstrate the geometric interpretation. 

I sometimes use analogies or jokes to help the students better understand the material.  Ian Corey-Boulet notes in his observation that I use the metaphor of how chain rule is like an onion.  I get a lot of groans with my joke about what the integral of cabin dcabin is.  Students natural say log cabin but the answer is of course houseboat since they forgot to add the C.  While this joke is cringeworthy, it also helps them to remember to add +C to end of their integrals.  Formal language and definitions are slowly introduced over time to build up the abstract intuition.  To illustrate, I offer this comment from Jonathan Briggs’ observation: He is also careful to use formal math words that will show up later on but writes them out, things like “such that”, “for every”, “there exists” which all will eventually become symbols in math proofs at later stages of math education. This will make it easier for students to think in formal math language intuitively.  In another observation, he notes Students clearly see connection to prior concepts, “this is like recycling last trimester’s eigenvectors.” Lot’s of laughing – students making an analogy of math being like the marvel cinematic universe.

When time allows, students are taught several different methods to solve a problem.  I then make sure that I never actually require a certain method to solve a problem.  This approach gives no favoritism to one method over another and allows the students to employ the one that makes the most sense to them.  To further this connection, sometimes questions are given where students need to explain two different methods of solving the problem both make sense.  Here is an example from a question I wrote for a Calculus test a number of years ago and which has endured since with minor tweaks:

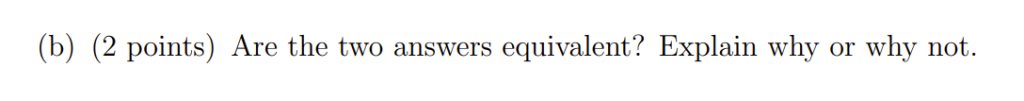
One goal I have is to always have an answer when a student asks why we are learning this.  To that end, I make a point of knowing where in the real world the material we learn shows up and try to give that context in class.  In Advanced Topics this year, I have had at least one application problem on each test and always vary the field that question falls in, with chemistry, physics, material science, engineering, and encryption questions all showing up.  Our students can help me out in this regard, as Molly Lori notes Addie says her dad works in Optimization. (Real-world extension of John’s class!).  One of my favorite examples of this is when I was asked about the real world application of volumes of revolution.  I had to do some research but the students (maybe for the wrong reasons) greatly enjoyed the story about where this technique comes from.  It turns out the scientist Kepler create the technique when trying to buy barrels of wine for his wedding and determining the usual method of finding the volume of the barrel was incredibly inaccurate.  The students enjoyed this so much they created a whole page in the collaboration space about this.

As John Stegeman noted in his observations, we also had nice discussion on the same topic about finding the volume of a Bundt cake and how this could be the final:

• Perhaps the funnest and funniest part of the class was the discussion of cake baking as a final assessment. 😊

Finally, I will note that the students seem to agree that I am effective in providing alternative course explanations.  Here are a sample of responses to the question what would I most compliment my teacher on:

• He’s very good at explainaing the material in different ways
• really good at explaining stuff when I ask questions
• Explaining the material thoroughly.
• Obviously knows a lot and is very good at explaining topics to make them easier to understand. Never been confused after asking a question.
• Being fun and explaining things clearly.
• His easy going nature and ability to explain things in multiple different ways.
• If I am confused and do not understand the topic he can explain it differently
• His incredible knowledge base on the content we’re learning which allowed him to make connections from new difficult content to past content that we already understood, making learning the new content much easier.
• He is able to explain stuff well in a visual way
• Explain concepts in depth and helping me understand things conceptually.
• I would compliment Dr. Kaminsky on how knowledgeable he is and how he can break down extremely concept concepts into bite-sized portions that we can easily pick up and understand!
• Being able to explain things differently for everyone to understand and having a great teaching pace so that I can fully comprehend everything.
• Is your willingness to help every problem that a students has, from simple small problems to large questions about the material.

(5) adapts instruction based on formative assessment

Since I teach classes that are mostly junior or senior level, I probably do this the least of any math teacher here.  Having taught in college before, I know that instruction at the college level does not really adapt based upon the results of an assessment.  Instead, if students are struggling, the burden is placed upon them to reach out for support.  Professors do not reach out to students or tell them to come to office hours.  Part of my goal is to get them used to this environment.  Students know I am available for help and will do what I can but the onus is on them to ask.  Once you get beyond Calculus, most of the students taking math here are self-selecting to be in math, which means they are generally more interested and comfortable in math.  Therefore, supporting students tend to occur less at the classroom level and more at the individual level.  This trend will continue in college, so it is important for students to get practice in reaching out for support when they need it.

That is not to say that I do not adapt my instruction based on feedback I receive from the class.  I place a number of structures in my class to give me information on how students are doing.  Homework is assigned whenever we cover new material for students to practice on.  Solutions are provided for the homework and it is on the students to check their work against the them.  Homework is graded for completion, not accuracy, but I do an overview of every students homework checking for repeated mistakes as well as mistakes being made by multiple students.  If I see a student making repeated mistakes, I will make a comment in Canvas for them to read, whereas if it is mistake being made by multiple students, I will be sure to address it in class.

Since the pandemic, I have employed exit tickets in my class.  These are quick five minute questions given at the end of class that I do grade for accuracy.  The answers allow me to get a quick snapshot of the understanding of the class and if I am seeing some major misunderstanding, I can correct it at the beginning of next class.  These exit tickets are also collaborative, so students can bounce ideas off each other and confirm their work with their neighbors.  Hearing these conversations is actually more valuable than grading, as any confusion about the material covered in class is usually cleared up pretty quickly through these peer to peer interactions.

In Calculus this year, we have adopted a curving system which requires students to correct their test to get their curved score.  I have coupled that with a grading system first introduced to EPS by Sarah Aguiar where student mistakes are highlighted on the test but the grade is not shown.  Instead, it is in Canvas, which is not muted until after the class the test is returned.  Students have time in class to do their corrections even though they do not know the score they got.  This places the emphasis on actually correcting their work and understanding their mistakes.  Molly Lori clocked that one student thanked me for this opportunity for growth when I first introduced this new form of correcting the test.

Furthermore, if a student scores poorly on a particular exam, I always assure them that I take a holistic view of their progress and will take into account that a student can just have a poor day when assigning final grades to the class.